杨海 教授、博士、硕士生导师
研究领域：丢番图方程、解析数论、数论及其应用
电子邮箱：xpuyhai@163.com
■个人简介
杨海，男，2010年到BET体育365投注官网工作，分别于2013年和2018年晋升为副教授与教授，2012年聘为硕士生导师。
长期从事丢番图方程、解析数论、数论及其应用等领域的研究，以第一作者（通讯作者）在国内外期刊上发表学术论文50余篇，其中被SCI收录16篇，CSCD核心期刊10多篇；主持或参与国家级、省部级基金、厅局级基金10余项；2016年入选校青年学术骨干。
教育背景及工作经历：
201008-至今，BET体育365投注官网，教师
201502-201602，加拿大英属哥伦比亚大学，数学系，访问学者
201205-201502，陕西师范大学，数学博士后流动站
200409-201007，西安交通大学，BET体育365投注官网，博士
200109-200406，延安大学，数学与计算机学院，硕士
199709-200106，延安大学，数学与计算机学院， 本科
荣誉获奖：
2011年，陕西省首届青年数学教师讲课比赛 “优秀示范奖（一等奖）”
2012年，BET体育365投注官网2011-2012学年优秀教师
2014年，陕西省数学会2014年青年教师“优秀论文二等奖”
2017年，BET体育365投注官网2015-2016,2016-2017学年“师德先进个人”
2020年，第十二届全国大学生数学竞赛“优秀指导教师”
2020年，BET体育365投注官网2019年度 “学习强国”平台学习活动“先进个人”
■教学工作
主讲课程：
本科生《数学分析》、《高等数学》、《线性代数》、《概率论与数理统计》、《专业导论》、《信息安全的数学基础》等多门课程。
研究生《解析数论》、《丢番图方程》、《计算数论》等课程。
教育教学：
1. 研究生教改项目《数学学科拔尖人才培养的探索与实践》, 2020年，主持
2. 指导研究生获数学建模竞赛国奖三等奖1项、高校数学密码挑战赛西北赛区一等奖1项，二等奖2项；指导本科生参加数学建模竞赛获省一、二等奖多项，获全国大学生数学竞赛国家三等奖2项，省一、二等奖多项；2015-2021年，指导教师
3. 省部级教育教学成果二等奖、三等奖各1项，校级特等奖1项，2020年，参与
■科研及社会服务
主持或参与的科研项目：
1. 国家自然基金：关于Dedekind和的混合均值与互反公式的研究(No. 11226038), 201301至201312，主持
2. 陕西自然科学基金：几类经典指数不定方程问题的研究(No. 2017JM1025), 201701至201812，主持
3. 陕西自然科学基金：几类椭圆曲线整数点问题的研究(2021JM443), 202101至202212，主持
4. 陕西教育厅基金：关于Dedekind和与数论中若干方程可解性问题的研究(No. 11JK0472), 201107至201306，主持
5. 陕西教育厅基金：数论中几类丢番图方程可解性问题的研究(No. 14JK1311), 201401至201609，主持
6. 陕西教育厅基金：数论方法在信息安全算法中的应用(No. 17JK0323), 201701至201812，主持
7. 国家自然基金：量子态分类与量子绝热逼近中的算子论方法(No.11371012)，201401至201712，参与
8. 横向项目：井下换热模型计算（No.2022KJ-301，10万），202205至202512，主持
代表性成果：
1.Hai Yang，P. G. Walsh. On a Diophantine problem of Bennett. Acta Arith. 2010，145(2): 129-136.
2.Hai Yang. A hybrid mean value of the Dedekind sums. Czechoslovak Mathematical Journal, 2010，60(4): 1055-1063.
3.Hai Yang，Ruiqin Fu. On trinomials having irreducible quadratic factors. Periodica Mathematica Hungarica. 2014，63(4): 375-383.
4. 付瑞琴，杨海*.一个特殊的Gauss和以及它的上界估计.数学学报，2014，57(6):1141-1146.
5.Hai Yang，Ruiqin Fu. An upper bound for least solutions of the exponential Diophantine equationD1x2−D2y2=λkz.International Journal of Number Theory. 2015，11(4), 1107-1114.
6.Hai Yang，Ruiqin Fu. A note on Jesmanowicz' conjecture concerning primitive Pythagorean triples. Journal of Number Theory. 2015，156(4), 183-194.
7.杨海，付瑞琴. Fermat素数Jesmanowicz猜想，数学进展，2017，46(6):853-862.
8.杨海，侯静，付瑞琴. 关于三次Diophantine方程
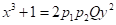的可解性，中山大学学报，2017，56(5):30-33.
9.杨海，付瑞琴，任荣珍.关于商高数的Jesmanowicz猜想.数学杂志, 2017，37(3):506-502.
10.Hai Yang，Ruiqin Fu. The exponential diophantine equationxy+yx=z2via generalization of the Ankeny–Artin–Chowla conjecture. International Journal of Number Theory. 2018, 14(5), 1223-1228.
11.Hai Yang，RuiqinFu. An open problem on Jesmanowicz conjecture concerning primitive Pythagorean triples, Glasnik Mathematicki. 2019, 54(74): 271-277.
12.Hai Yang，Ruiqin Fu.Integral points on the elliptic curvey2=x3–4p2x，Czechoslovak Mathematical Journal，2019, 69(3): 853-862.
13.Hai Yang，Ruiqin Fu. Complete solutions of the simultaneous Pell’s equationsx2–(a2–1)y2= 1 andy2–pz2= 1. International Journal of Number Theory. 2019, 15(5), 1069-1074.
14. Ruiqin Fu,Hai Yang*，On the generalized Ramanujan-Nagell equationx2+(3m2+1)=(4m2+1)n，Indian Journal of Pure and Applied Mathematics，2022，53(1), 222-227.
15.Hai Yang，RuiqinFu.A further note on Jesmanowicz' conjecture concerning primitive Pythagorean triples，Mediterranean Journal of Mathematics，2022，19(2), 57-64.
兼职情况:
美国数学评论（Math review）评论员；国内外多个数学期刊杂志审稿人；陕西省数学会青年工委会委员
